Here is something slightly different that I’ve done with Sonic Pi - it’s not so much about the Sonic part of Sonic Pi, but about the visuals.
Note: I have included some pictures taken from a book, to compare with the visuals generated in Sonic Pi. I hope this would count as fair use under copyright law, but if it’s an issue I’d be happy to remove them and replace with them with versions entirely generated in Sonic Pi, without the book figures for comparison.
When Sonic Pi first added the Lissajous scope I had a lot of fun playing around generating Lissajous figures. I thought I had posted about it somewhere at the time, but I can’t find the post now, so maybe I’m misremembering (or maybe it was on another platform before in-thread?). Anyway, the screen recordings I made at the time are still up on Vimeo - here with various different synths and tunings, and here using only sine waves and simple rational frequency ratios. The code for both is on github, here and here respectively.
Some time later, I forget where, I saw somebody recommend a book called Harmonograph: A Visual Guide to the Mathematics of Music by Anthony Ashton. It’s a small book (pocket sized, and only around 60 pages), but it’s beautifully made, and I would also highly recommend it to anyone who is even vaguely interested in the mathematics of music.

It takes a look at a Victorian device called the Harmonograph, which uses a pen and paper linked to pendulums to draw figures or graphs, and the relation of this device to musical harmony.
There are a lot of figures in the book, and I started wondering whether it would be possible to reproduce them with the Lissajous scope in Sonic Pi.
There are two types of Harmonograph - called lateral and rotary. In a lateral Harmonograph two pendulums, one linked to the pen, and the other to the paper, oscillate perpendicular to each other. This generates essentially the same Lissajous figures that I already mentioned above.
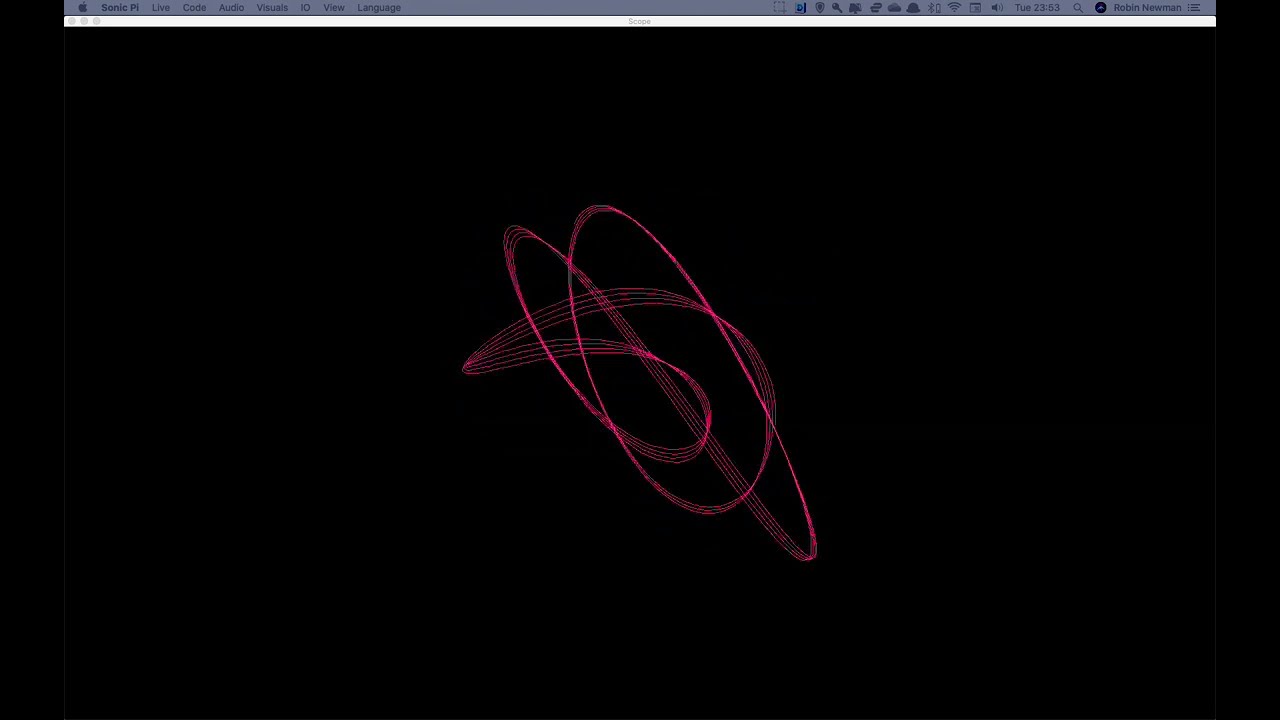
In a rotary harmonograph however, the two linear pendulums both control the pen, while a third rotary pendulum moves the paper in a circular motion. Generally, the two linear pendulums oscillate at the same frequency, therefore generating a circular motion, and this interacts with the circular motion of the paper (possibly at a different frequency and/or amplitude), generating many different and beautiful patterns.
In order to recreate these patterns in Sonic Pi, in theory I should only need two pairs of sine wave synths to generate two circular motions and add them together. However, to get it to work reliably, I found I needed good control over the relative phases of each pair of sine waves, and this was not really feasible (at least as far as I could manage) with separate synths.
So, I decided to create my own synth especially for Lissajous and Harmonograph figures. It essentially consists of two sine waves; one sent to the left, and the other to the right channel.
There are parameters to control the relative frequency, phase and amplitude of each sine wave. I’ve made the source code as well as the compiled synthdef available as a gist here, along with all the code for the figures in this post, in case anyone is interested to try it out (@samaaron I’d also be happy to open a PR if you think this might be something that could be added to Sonic Pi?).
Using a single lisa synth to simulate the two perpendicular pendulums I was able to recreate all the lateral Harmonograph figures. Here you can see some figures from the book with the corresponding Sonic Pi screen captures overlaid:
To recreate the rotary Harmonograph figures, I just had to use two lisa synths at the same time. One slightly confusing thing that took me a bit of trial and error to figure out, was that the figures labelled “inv. amp.” meant that one of the synths had to be half the amplitude of the other (not 180 degrees out of phase, as I initially assumed). Here you can see some (according to the book, these figures originally come from Sir Thomas Bazley’s Index to the Geometric Chuck, 1875, so should be out of copyright by now), again with the screen captures from Sonic Pi overlaid:
All the figures shown up to here had constant amplitude. However, a number of figures showed what you get as you allow the pendulums to decay in amplitude over time, creating more complex spiralling patterns. To recreate these, in theory I’d just have to set the release parameter on the synths. However, it was a bit tricky to get it working in a visually appealing manner. In the end I set the release to something in between 1/10 to 1/20 of a second, and captured a screen recording. The effect was spread over a handful of frames which I merged together afterwards to create the images. Here you can see the results of trying to recreate some of the figures from the book:
I didn’t overlay these ones since they are less precise reproductions of the figures than the previous ones, so they don’t line up quite so well.
There are quite a few more figures in the book that I may try to recreate in the future, but I wanted to post what I have so far, as I thought it was pretty cool, and maybe it might inspire someone else to experiment with this. I’d love to see what other people come up with!